Elementi di geometria vedica trascendentale

Introduzione

Il sistema vedico prevede due sottosistemi: il sistema Sankhya e il sistema Yoga. Essi sono reciprocamente complementari, e conducono agli stessi risultati.
Il sistema Sankhya si avvantaggia della manipolazione dei numeri quando sia disponibile una configurazione dimensionale, il sistema Yoga si occupa delle configurazioni dimensionali, posto che vi siano delle procedure computazionali.
Per la ricerca dello spazio reale di ordine 4 in geometria vedica, è necessario disporre di:

1. Artifici numerici di ordine 4
2. Uno spazio che ammetta quattro dimensioni

Spazio reale di ordine 4

• La ricerca di questa caratteristica è dapprima orientata all’ottenimento dell’esperienza mentale della rappresentazione di un solido regolare di ordine 4, la cui manifestazione iconica è Brahma.
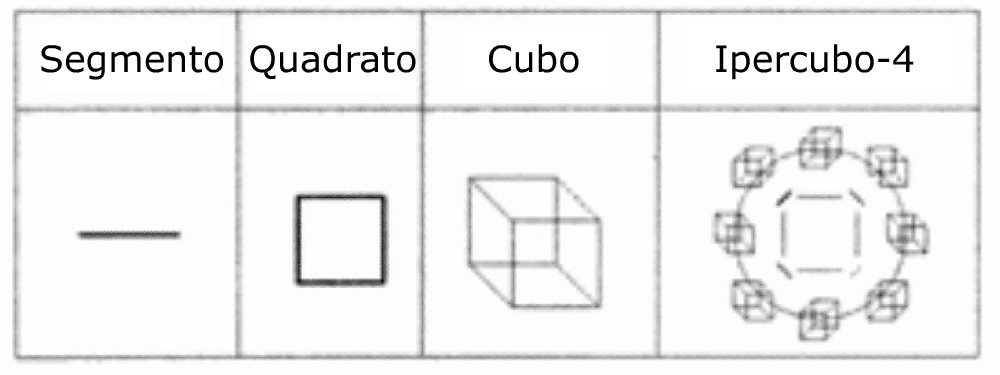
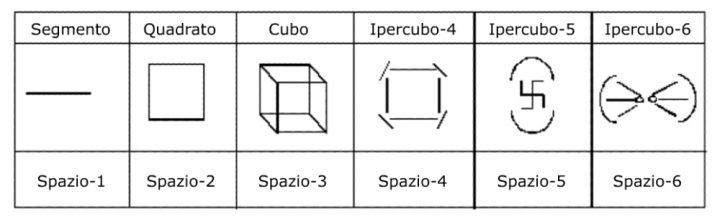
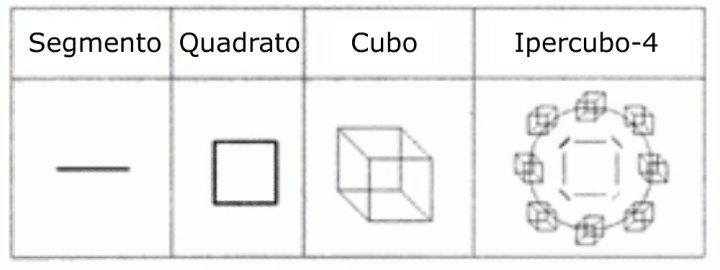
  Questa rappresentazione, denominata ipercubo-4, è il quarto membro della sequenza dei solidi regolari rappresentativi degli spazi dimensionali, essendo i primi tre l’intervallo o segmento, il quadrato e il cubo, rispettivamente i corpi regolari di ordine 1, 2 e 3.
• Il successivo approccio alla definizione dello spazio reale di ordine 4 e dell’impianto geometrico dell’ipercubo-4 è l’esperienza mentale del centro del cubo, cioè dell’origine dello spazio di ordine 3.
  Ciò equivale alla visualizzazione di un cubo che viene diviso in otto cubi da un sistema di riferimento tridimensionale avente origine al centro del cubo.
• Il terzo passo per la comprensione dell’esistenza dello Spazio reale di ordine 4 consiste nel comprendere che la traiettorie di un punto, di un segmento, di una superficie e di un volume portano rispettivamente a Spazi reali di ordine 1, 2, 3 e 4. Grazie alla rimozione di costrutti mentali illusori è possibile concepire lo Spazio reale di ordine 3, che è lo spazio tridimensionale di cui facciamo esperienza nell’ordinario stato di coscienza non-centrato, emerge dal movimento di superfici. Di conseguenza lo Spazio reale di ordine 4 deriva dal movimento di volumi.
• Il passo successivo consiste nel passaggio dallo stato macroscopico degli oggetti fisici allo stato microscopico delle entità.
• Il quinto passo per avere esperienza di questo Spazio reale di ordine 4 come stato microscopico sottile è di trascendere lo stato di veglia per raggiungere in piena consapevolezza lo stato di sogno.
  L’origine dello Spazio di ordine 4 è lo Spazio reale di ordine 5.

Esistenza di spazi di ordine superiore

Proviamo a concepire il segmento (lo spazio monodimensionale) come la traccia prodotta da un punto in movimento; potremmo quindi considerare la superficie di un quadrato (lo spazio bidimensionale) come la traccia prodotta da un segmento in movimento e, allo stesso modo, è possibile visualizzare il volume di un cubo (spazio tridimensionale) come prodotto dal movimento di una superficie quadrata.
A questo punto potremmo chiederci quale possa essere la traccia prodotta dal volume di un cubo in movimento: la naturale risposta è un ipercubo-4, ossia un oggetto del dominio ipersolido (spazio quadridimensionale).
Siamo circondati da solidi in movimento.
Perfino noi stessi, quando ci muoviamo, creiamo spazio quadridimensionale col nostro movimento.
Di conseguenza lo spazio in cui ci muoviamo liberamente non è uno spazio tridimensionale, ma è in realtà uno spazio quadridimensionale, in cui coesistono dimensioni di ordine superiore.
Il movimento di un ipervolume (un ipercubo-4) creerà uno spazio pentadimensionale, e così via, permettendoci di generalizzare il concetto che un oggetto di dimensione n, col suo movimento, creerà uno spazio di ordine n+1.
Per avere una chiara esperienza mentale degli spazi di ordine superiore al 3 è necessario perfezionare la propria visione interiore considerando il movimento di un punto, di un segmento, di una superficie e di un volume.

Fonti

Vedic geometry course di S.K. Kapoor
Vedic Ganita