L’assioma della dimensionalità
Introduzione
La dimensione di uno spazio riflette la diversità dei suoi abitanti, i gradi entro cui possono muoversi, espandersi, contrarsi, crescere o vibrare, ma ogni grado di movimento deve essere limitato alle variazioni lungo un parametro unidimensionale. C’è un aspetto fondamentale, un assioma implicito nascosto nella pratica della geometria euclidea, un assioma che, se cambiato, potrebbe dar luogo a una nuova visione creativa della geometria: l’assioma della dimensionalità.
In una descrizione affascinante dei più recenti sviluppi della Teoria delle Stringhe, considerata il Santo Graal di una descrizione intellettuale e logica della natura, viene illustrato chiaramente il ruolo di primo piano della geometria negli attuali sviluppi in fisica teorica. Secondo le più recenti ricerche noi vivremmo in un universo che può essere descritto come un continuum spazio-temporale 11-dimensionale in cui tutte le dimensioni, tranne le tre dimensioni spaziali e quella temporale, sono confinate in una regione (attualmente) non osservabile. Dal momento che attualmente non esistono mezzi sperimentali per determinare la natura precisa del continuum spazio-temporale matematico multidimensionale entro il quale il nostro Cosmo si presume che esista, i ricercatori tendono a fare affidamento su principi di simmetria e logica per guidare i loro sviluppi.
Questo universo matematico è abitato da molte specie meravigliose ed esotiche, come ad esempio stringhe unidimensionali vibranti in spazi di Calabi-Yau a sei dimensioni arrotolate. Più recenti sviluppi, promossi dalla cosiddetta seconda rivoluzione della super-stringa, hanno dato luogo alle ancor più esotiche p-brane, in cui le stringhe unidimensionali sono riconducibili a una concezione più generale di vibrazioni in molte dimensioni, e oggetti denominati zero-brane, oggetti che a grandi distanze si comportano come particelle puntiformi, ma a quanto pare hanno una struttura molto definita alla scala subatomica.
C’è però un’altra versione della geometria, in cui i punti hanno una certa struttura, e questo porta a discutere un aspetto fondamentale della geometria, che non ha mai ricevuto un serio esame perché è un assioma nascosto, “l’assioma della dimensionalità”.
Dimensioni Euclidee
Quando vogliamo descrivere le interazioni matematiche un passo fondamentale in questo processo è quella di definire in forma esatta l’ambito entro il quale queste interazioni avvengono.
Pertanto, la prima linea in qualsiasi trattato di matematica segue spesso la convenzione: “considerare l’insieme di …”, oppure: “considerare un …”, dove ai puntini di sospensione di solito corrisponde un gruppo ben definito di oggetti matematici su cui si può operare per produrre un nuovo insieme di oggetti, e quindi sviluppare un particolare teorema o tesi.
Qui possiamo affermare che la geometria ha come arena un continuum multidimensionale, che può essere classificato in un certo numero di modi diversi.
Una delle più importanti categorizzazioni descrive lo spazio come un continuum n-dimensionale in cui ogni elemento dello spazio richiede una n-tupla di numeri reali indipendenti per una sua completa descrizione. Inoltre è necessario definire una origine per quello spazio, cioè un sistema di riferimento globale in cui ciascuno dei valori della n-tupla è 0. In questo modo la dimensionalità del nostro spazio è definita da n copie di uno spazio lineare o 1-dimensionale. Questa categorizzazione dello spazio ha dato origine a importanti campi della computazione matematica, ma gli effetti completi di questa definizione non sono stati ancora pienamente esplorati.
Gli spazi lineari indipendenti che compongono lo spazio tridimensionale hanno una struttura semplice, essendo in un modo o nell’altro assimilabili alla linea reale. Anche se le basi del nostro continuum multidimensionale possono essere esse stesse descritte come funzioni, esse sono ancora considerate monadiche, ed aventi un singolo carattere. Questa descrizione ha servito molto bene la matematica, ma non è l’unico modo in cui possono essere definite le dimensioni di uno spazio.
Esiste un’alternativa che può portare a una fonte molto ricca di nuovi metodi e tecniche computazionali in matematica, e in geometria in particolare.
Dimensioni Vediche
La descrizione precedente del concetto di dimensione assicura che la caratteristica primaria di spazi con una struttura simile riguarda la cardinalità degli spazi dimensionali.
Ogni spazio tridimensionale è un’estensione lineare di una monade, basandosi sulle trasformazioni di Logica Lineare Booleana.
Un semplice cambiamento nella concezione della dimensione conduce ad una ricca fioritura di potenziali strutture matematiche. Questo cambiamento è stato sviluppato da S. K. Kapoor, che sostituisce l’assioma nascosto della dimensionalità, secondo cui “la dimensionalità di ogni spazio dimensionale è uno spazio lineare unidimensionale monadico“, con l’assioma vedico secondo cui “l’ordine del spazio dimensionale è di due ordini inferiore all’ordine del dominio spaziale“. Così se stiamo considerando un dominio spaziale vedico Vn, vale a dire un continuum multidimensionale con dimensione n, i suoi spazi dimensionali sono n×Vn-2, cioè n spazi autonomi ciascuno di dimensionalità n-2.
Il percorso per realizzare tale modifica della descrizione concettuale della dimensione è discusso in dettaglio da S.K. Kapoor, che approfondisce sulla correlazione tra le varie strutture degli spazi reali multidimensionali e la loro rappresentazione in vari aspetti della letteratura vedica.
In sintesi, dalla sua analisi della letteratura vedica, Kapoor teorizza una quadruplice struttura per ogni dominio spaziale, composta da dimensione, margine, dominio e origine. Questa ripartizione è visualizzabile se consideriamo i corpi regolari rappresentativi per ogni spazio, e le loro interrelazioni.
Corpi Regolari Rappresentativi
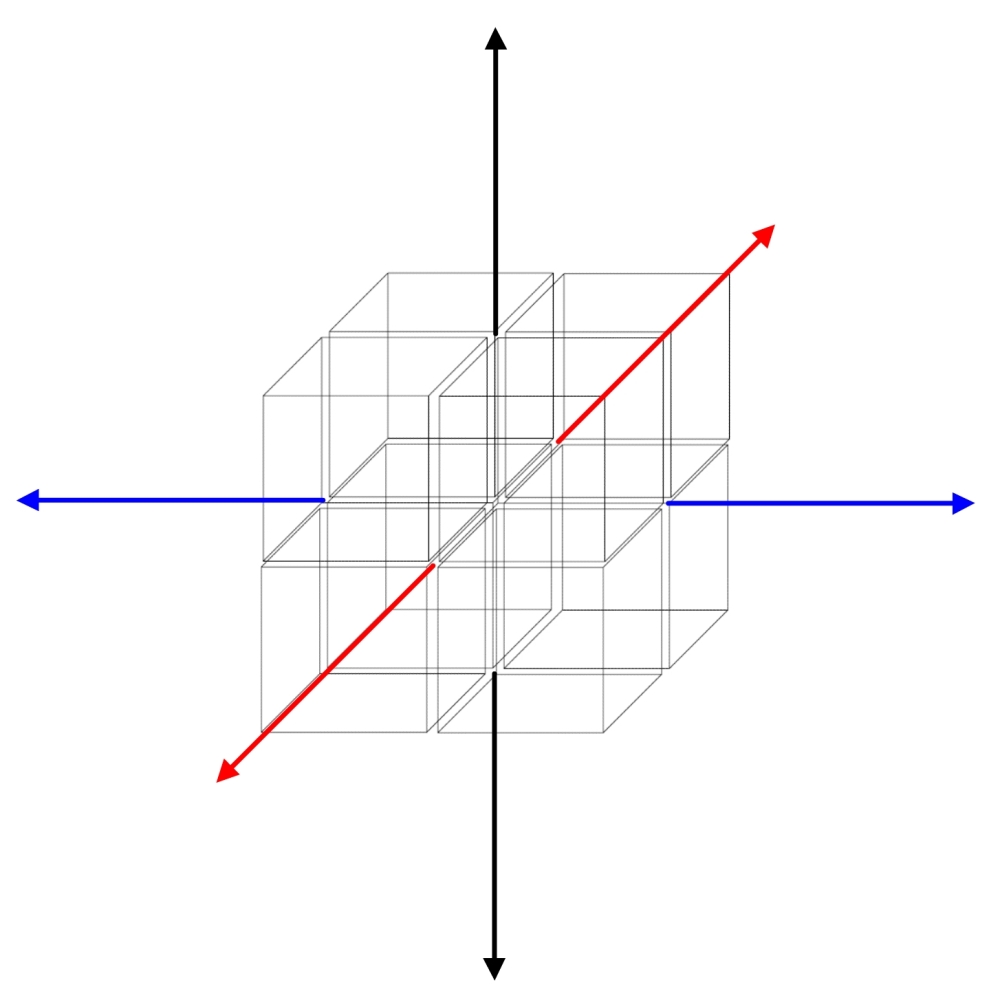
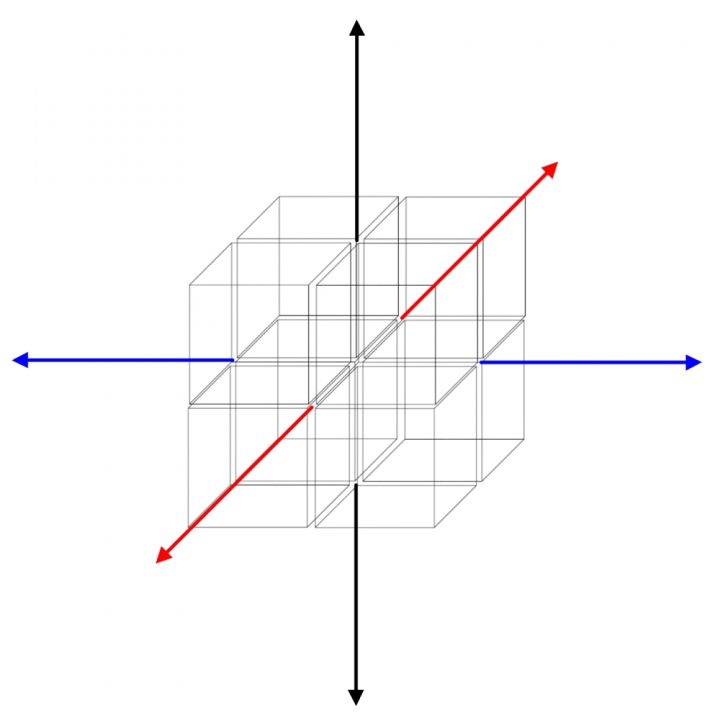
Quando consideriamo uno spazio unidimensionale, la rappresentazione più naturale per questo spazio è un intervallo unitario, similmente per uno spazio bidimensionale la rappresentazione più naturale è un quadrato unitario, e per uno spazio tridimensionale la rappresentazione più naturale è un cubo unitario. Ognuno di questi corpi regolari rappresentativi può essere derivato in modo sequenziale, come la traccia che un corpo di dimensione n produce muovendosi in uno spazio di dimensione n+1.
Partendo da un punto a-dimensionale, il suo movimento traccia un intervallo monodimensionale, il cui movimento genera una superficie bidimensionale, il cui movimento produce un volume tridimensionale. In ognuno di questi casi il movimento avviene lungo una dimensione matematica non coperta dalla estensione del corpo regolare, come illustrato nella Figura 1, in cui si assume che a sia l’unità di lunghezza attraverso cui un corpo geometrico regolare rappresentativo si muove per generare il corpo geometrico di ordine successivo.
Una linea che si muove nello spazio in una direzione diversa da se stessa, uscendo da se stessa, altrimenti si prolungherebbe solamente, lascia la traccia del suo movimento come un piano.
Un piano che si muove nello spazio in una direzione diversa da se stesso, uscendo da se stesso, lascia la traccia del suo movimento come un solido.
Di conseguenza quando un oggetto tridimensionale si muove nello spazio in una direzione diversa da se stesso, quindi fuori da se stesso, lascia la traccia del suo movimento in una dimensione di ordine 4.
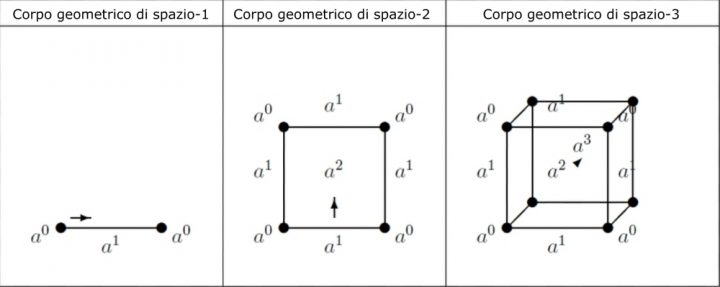
Notiamo anche che i corpi regolari rappresentativi possono essere rappresentati in successione dalle seguenti espressioni algebriche:
r0 = a0 Intervallo dimensionale 0 - punto r1 = a1 + 2a0 Intervallo dimensionale 1 - linea r2 = a2 + 4a1 + 4a0 Intervallo dimensionale 2 - quadrato r3 = a3 + 6a2 + 12a1 + 8a0 Intervallo dimensionale 3 - cubo
La questione ora è di sapere qual è la struttura geometrica di un corpo regolare rappresentativo di ordine 4, e come può essere generato.
Innanzitutto possiamo dire che il corpo regolare rappresentativo di ordine 4 è un ipercubo generato
spostando il cubo, che è un corpo geometrico corrispondente all’espressione algebrica r3 = a3 + 6a2 + 12a1 + 8a0, lungo una dimensione matematica iperspaziale distinta da ciascuna delle dimensioni spaziali attualmente visibili.
Notiamo che la manifestazione di un corpo regolare di odine n è il prodotto del corpo regolare rappresentativo di ordine inferiore per (a + 2).
Questo processo manifestativo può essere riassunto con la seguente notazione simbolica:
r0 → M → r0 (a + 2) = r1 = (a0) (a + 2) = a1 + 2a0
r1 → M → r1 (a + 2) = r2 = (a1 + 2a0)(a + 2) = a2 + 4a1 + 4a0
r2 → M → r2 (a + 2) = r3 = (a2 + 4a1 + 4a0)(a + 2) = a3 + 6a2 + 12a1 + 8a0
in base alla quale possiamo stabilire che il prodotto della manifestazione M di un cubo è:
r3 → M → r3 (a + 2) = r4 = (a3 + 6a2 + 12a1 + 8a0)(a + 2) = a4 + 8a3 + 24a2 + 32a1 + 16a0
che è l’espressione algebrica che rappresenta l’ipercubo generato dal movimento di un cubo in una dimensione matematica iperspaziale indipendente dalle dimensioni visive esistenti.
Un’analisi completa degli spazi di dimensioni superiori, così come rappresentati nella letteratura vedica, ha permesso a S. K. Kapoor di dedurre che questa particolare forma generazionale è valida anche per la generazione di corpi regolari rappresentativi di dimensioni ancora superiori, permettendo di generalizzare con la seguente notazione:
rn-1 → M → rn-1 (a + 2) = rn = (a + 2)n
che ci permette di stabilire con esattezza i costituenti di un corpo regolare rappresentativo corrispondente ad un qualsiasi spazio di ordine n.
L’interpretazione vedica di questa espressione dà luogo ad un continuum di spazi molteplici in cui la transizione da uno spazio all’altro avviene attraverso trascendenza all’origine del dominio, intendendo come origine un contenuto spaziale specializzato con un collegamento diretto allo spazio dimensionale superiore. Quindi l’origine dello spazio tridimensionale è concepito come un elemento quadridimensionale, attraverso cui, per trascendenza, possiamo accedere a uno dei componenti di contorno dell’ipercubo a quattro dimensioni. Questo è in evidente contrasto con l’attuale prescrizione dimensionale euclidea, dove tutti i punti nel dominio vengono considerati uguali, e secondo cui l’unico modo per trascendere ad uno spazio di dimensione superiore è quello di muovere l’intero spazio.
Il continuum geometrico è espresso come strato manifestativo o strato fenomenico composto da 4 componenti consecutive. Uno strato manifestativo di ordine n può essere rappresentato come sotto:
| primo componente | secondo componente | terzo componente | quarto componente |
|---|---|---|---|
| Dimensione | Struttura | Dominio | Origine |
| (n-2) | (n-1) | n | (n+1) |
Lo strato manifestativo di ordine 3, proprio del nostro spazio tridimensionale che percepiamo nello stato di veglia, sarà rappresentato così:
| Dimensione | Struttura | Dominio | Origine |
| (3-2)=1 – Segmento unitario | (3-1)=2 – Superficie unitaria | 3 – Volume unitario | (3+1)=4 – Spazio di ordine 4 |
L’inclusione dell’origine del dominio come elemento separato e con proprietà distinte porta alla prescrizione di un continuum matematico di spazi necessari per la descrizione completa di un qualsiasi spazio multidimensionale.
Possiamo vedere che gli elementi di un dominio vedico sono composti da contenuti spaziali n-dimensionali, e questo contrasta con un dominio euclideo, dove ciascuno degli elementi, cioè i punti, sono considerati come contenuto zerodimensionale, e possono essere definiti solo da una posizione, intesa come n-tupla. Quindi non è possibile distinguere esplicitamente, in base al contenuto interno, tra i punti in un dominio euclideo, e i punti sui suoi margini.
I punti sui margini o punti di confine sono normalmente descritti utilizzando una qualche forma di equazione di vincolo, in altre parole utilizzando condizioni che sono esterne alla descrizione dei punti stessi.
Nel caso di un dominio vedico tale distinzione viene facilmente incorporata nella prescrizione della dimensione, in quanto l’ordine dei contenuti spaziali è diverso sia in termini di cardinalità delle dimensioni del punto che in termini di dimensionalità degli spazi dimensionali sottostanti.
Costituenti di uno spazio vedico
Quando consideriamo la prescrizione dimensionale in uno spazio euclideo n-dimensionale En, l’attuale n-tupla che rappresenta la dimensione è una descrizione della posizione in En di un punto a-dimensionale, e si riferisce alla misurazione di n-parametri necessari a descrivere precisamente il punto.
In generale, secondo la prescrizione dimensionale vedica, le n-tuple di parametri utilizzati
per descrivere un elemento di uno spazio vedico Vn sono qualitativamente differenti. Questo perché ciascuna delle n-tuple è essa stessa un elemento di uno spazio vedico Vn-2, uno spazio di dimensionalità n – 2.
Ciò dimostra che, mentre gli elementi di uno spazio euclideo sono punti zero-dimensionali, gli elementi di uno spazio vedico hanno un struttura spaziale intimamente legata allo spazio dimensionale sottostante. Così è possibile dire che gli elementi o punti di un dominio vedico Vn sono delle unità strutturate composte da n unità di dimensioni inferiori.
Vediamo come questa differenza di prescrizione influenza la nostra percezione dello spazio euclideo E3, e del dominio vedico V3. In entrambi lo spazio tridimensionale è lineare, essendo lo spazio euclideo composto da E1 – o la linea reale R, e quello vedico da V1. Poiché ogni punto E3 è rappresentato come tripla (x, y, z) di numeri reali, i punti appartenenti a E3 sono composti dal prodotto cartesiano E1 × E1 × E1.
In modo analogo gli elementi di V3 possono essere descritti come triple (x1, y1, z1), ma in questo caso ciascun elemento a1 non è un numero reale R ma un contenuto spaziale esteso V1. Così anche se usiamo un concetto simile al prodotto cartesiano, la nozione estesa degli elementi che compongono V1 implica che i componenti del dominio vedico V3 = V1 x V1 x V1 hanno un carattere esteso.
La differenza fondamentale tra gli elementi di E1 e V1 consiste nel fatto che nel dominio euclideo i singoli elementi sono dei punti zero-dimensionali, mentre gli elementi costituenti del dominio vedico sono elementi spaziali monodimensionali.
Muovendo un corpo tridimensionale nel dominio iperspaziale V4, vediamo che V4 = V2 x V2 x V2 x V2, il che implica che il contenuto spaziale del dominio V4 può essere rappresentato da una quadrupla (w2, x2, y2, z2), ciascuna delle cui componenti ha una estensione spaziale – essendo un elemento di dimensionalità V2. Questo contrasta notevolmente con lo spazio quadridimensionale euclideo E4 = E1 × E1 × E1 × E1 ×, dove gli elementi di E4 sono rappresentati dal quadrupla (w, x, y, z) dei numeri reali.
Fonti:
Brian Green, The Elegant Universe
S.K. Kapoor, Vedic Geometry
S. K. Kapoor, Fermat’s Last Theorem and Higher Spaces Reality Course
Brian G. Mc Enery, The Axiom of Dimensionality
https://sites.google.com/site/corknatcom/real-geometry-research/Axiom_of_Dimensionality.pdf